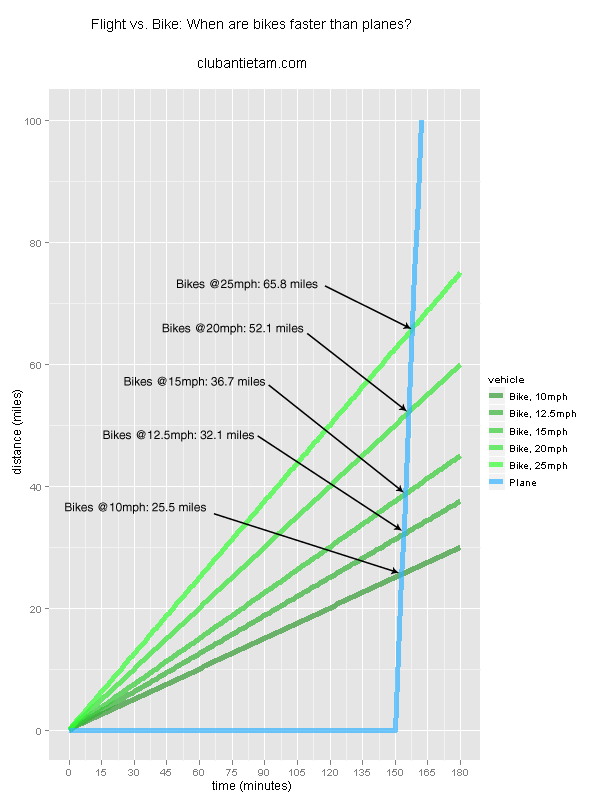
When our daughter was younger, I tried to quantify the "bumpiness" of her rides in strollers. We had two strollers, an older Bugaboo Bee (can't find a link to the older version) and a Thule Chariot Cougar (single, not double). We had the normal stroller attachment for the Chariot Cougar and the jogging attachment.



In addition to comparing the differences between strollers, I wanted to compare the "bumpiness" differences when walking and running.
Data collection was messy, as you'll see below, but hopefully the results are still interesting.
Measurements and Methods
I used an old iPhone 4S with an data logging app to measure its accelerometer output while the phone was placed in the bottom basket of the Bugaboo and in one of the front pockets of the Thule Chariot Cougar.
I used two different apps to record the data:
- Axelerom: For measurements of the Bugaboo and the Thule Chariot Cougar with stroller wheels
- xSensor: For measurements of the Thule Chariot Cougar with the jogging attachment
Both only recorded data when the phone screen was on, so I had to stop once and a while to make sure it was still recording. The Axelerom readings were taken at 5Hz and the xSensor at about 19-20Hz. The Axelerom readings were also somehow strangely rendered out of order in the data file. I had to resort the data by timestamp.
Upon analyzing the data, I realized that 5Hz wasn't fast enough to do anything other than measure acceleration. Even the xSensor measurements at 19Hz weren't that great. This was a bit of a problem, because I couldn't reliably measure the "jerk", or the rate of change of the acceleration. The jerk can have a large impact on the perceived quality of a ride. A good analogy is the difference between slowing down in a car at an intersection and abruptly letting off on the brake when the car comes to a stop rather than gently easing off of the brake pedal.
Coincidentally, I learned during research that 5Hz is roughly the resonant frequency of important parts of the body, and possibly the least comfortable vibration frequency to experience.
The measurements were taken on the sidewalks and streets in Oakland, California, mostly along the same ones for each stroller. I didn't take the exact same path or streets for each stroller though, so this is another potential source of variation.
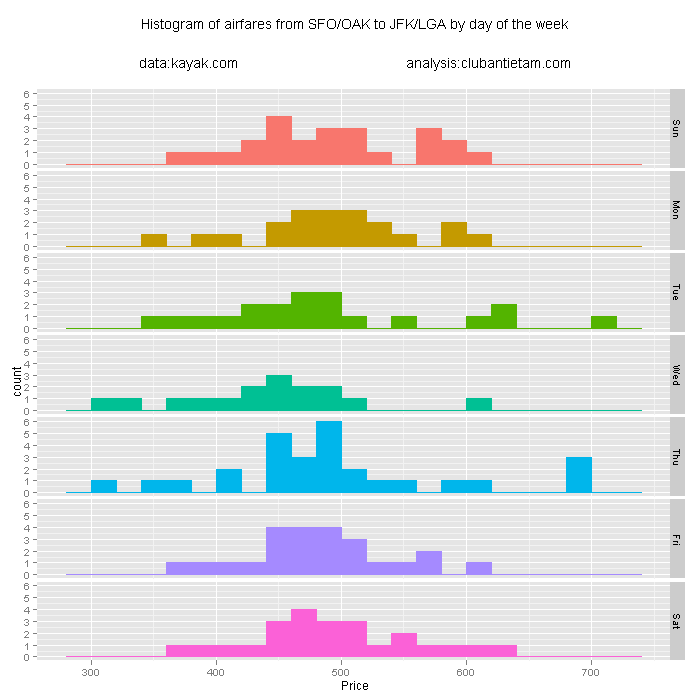
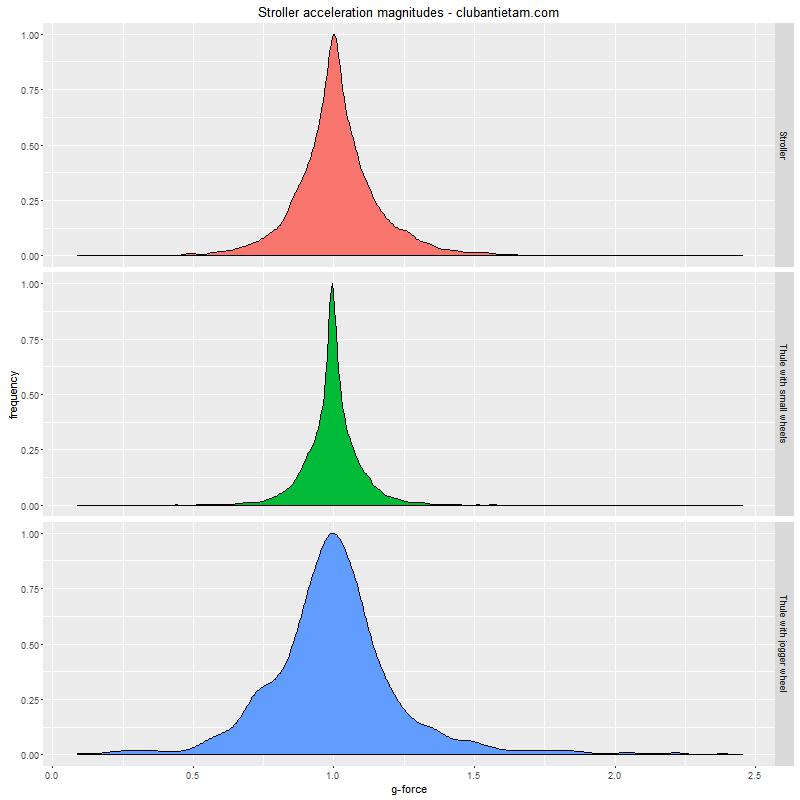
The smoothest ride was with the Thule Chariot Cougar

The Thule Chariot Cougar looks like a SUV next to the Bugaboo Bee stroller. It's got two 20" wheels with pneumatic tires and a suspension on the back. The Bugaboo's wheels are suspended too, but are much, much smaller.
One can observe the difference in forces measured in the stroller on the graph: the pointier the curve, the smoother and less bumpy the ride.
The numbers
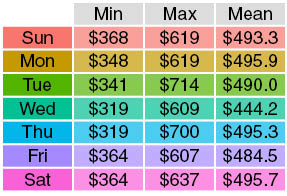
The Thule Chariot Cougar with the stroller wheels (in green in the chart above) provided the smoothest ride, with a minimum measured acceleration of 0.399 Gs and a maximum acceleration of 2.231 Gs. The standard deviation was 0.108 Gs.
The Bugaboo Bee was the next smoothest, with a minimum measured acceleration of 0.087 Gs (nearly freefall, for a split-second at least!) and a maximum measured acceleration of 2.452 Gs. The standard deviation was 0.165 Gs.
As one may expect, the bumpiest ride was with the Thule Chariot Cougar with the jogging attachment, recorded while running. I regret that I did not perform measurements while just walking with the jogging attachment installed to have that as a point of comparison. The minimum measured acceleration was 0.089 Gs, the maximum measured acceleration was 2.382 Gs, and the standard deviation was 0.242 Gs.
What does this all mean?
It was really interesting to find that the maximum and minimum recorded accelerations for the Thule Chariot Cougar with jogging attachment, while jogging, was similar to that of the Bugaboo Bee. And the Bugaboo Bee is a pretty smooth rolling stroller. I found that to be pretty reassuring. Though the ride while jogging was definitely bumpier, the maximum acceleration magnitude was smaller than that of the Bugaboo.
This was kind of just a fun exercise, but there are a couple of conclusions I came to:
- The Thule Chariot Cougar is a very smooth-riding stroller.
- Running with the Cougar's jogging attachment is sorta bumpy, but probably not way worse than the Bugaboo Bee.